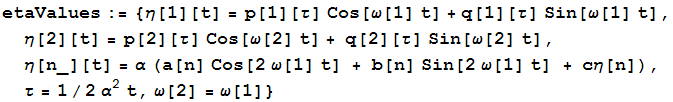
Eliminating η from η equations

Defining η

Note:  If the i in the equation is not defined, it is assumed to be greater than 2.

c has already been used so cη will be used as the third coefficient. etaValues stores the defination for the η function

In[10]:=

etaSubs is a list of transformation rules for η,η',η'' and η'''.This can be extended or shrunk from the segment {j,0,3} The three denotes a table with rules up to the third derivative.

In[11]:=

This evaluates etaEqn with etaSubs transformation rules.  NOTE:  This method of evaluating etaSubs requires real numbers for modes.  The subscripts extract the left and right sides of the requations and re-delete higher order terms

In[12]:=

In case a symbolic mode is warrented, the second equation will automatically be used.  This second definition will be slower.

In[13]:=

Eliminating powers of trig functions

These are the rules we'll be using to simplify etaEqn

In[14]:=

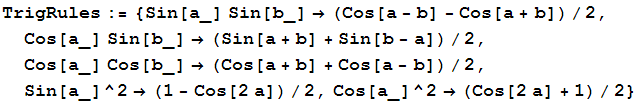
In[15]:=

Created by Mathematica  (June 26, 2006)